Об образовании Восьми триграмм (Багуа) рассказывается в И-Цзине, или “Книге Перемен”. В разделе “Да чжуань” разъясняется:
“В системе И-Цзина есть Тайцзи, или Великий Передел, который породил Две Формы (Лянъи). Эти Две Формы породили Четыре Символа (Сысян). Четыре Символа разделились дальше и породили Восемь Триграмм (Багуа)”.
Тайцзи – первая точка, возникающая из пустоты Уцзи. Она содержит движущую силу как динамичных, так и статичных состояний и является источником Инь и Ян. В статичном состоянии Инь и Ян сочетаются и образуют целое. Но в состоянии движения они разделяются и образуют Две формы (Лянъи).
Ян часто изображают графически в виде отрезка прямой или белого кружка. Инь обычно представляют в виде двух черточек с промежутком между ними или черного кружка. Различные символы Инь и Ян показаны на рис.1.

Рисунок 1
Свойства Двух Форм можно объяснить, используя напрвленную прямую (математическую ось). Приняв, что точка отсчета (ноль) – это Тайцзи. Мы получим Инь в отрицательном, а Ян – в положительном направлении:

Рисунок 2
Используя числовые обозначения, И-Цзин определяет Тайцзи как ноль, Ян – как единицу (нечетное число). А Инь – как двойку (четное число). Но еще эффективней можно показать свойства Инь и Ян в бинарной (двоичной) системе счисления. Определяя Ян как ноль, а Инь – как единицу. Или наоборот, мы можем объяснить теорию Тайцзи, Двух Форм и Четырех Символов (Сысян).
Четыре Символа – результат комбинаций Двух Форм. Два символа Ян, размещенные один над другим, называют Большой Ян (Тайян). Знак Инь над знаком Ян – это Малая Инь (Шаоинь). Два символа Инь один над другим – это Большая Инь (Тайинь). Знак Ян над знаком Инь образует Малый Ян (Шаоян). Схему Четырех Символов см. на рис.3.

Рисунок 3
Принцип Четырех Символов применим к любому объекту или ситуации. Все можно разделить на четыре взаимосвязанных части, учитывая качество и количество. Например, можно использовать символы инь и Ян для описания соотношения между населением и территорией различных стран. Используя верхнюю позицию для размещения символов населения (Ян — большое, Инь – малое), а нижнюю – для символов территории, получим четыре символа, показанных на рис. 4. Из диаграммы видно, что Китай и США можно считать странами Большого Ян, а страны типа Исландии – Большой Инь.

Рисунок 4
Геометрическим соответствием Четырех Символов являются четыре квадранта прямоугольной системы координат на плоскости. Как и в Двух Формах , Ян представляет положительное направление, а Инь – отрицательное:
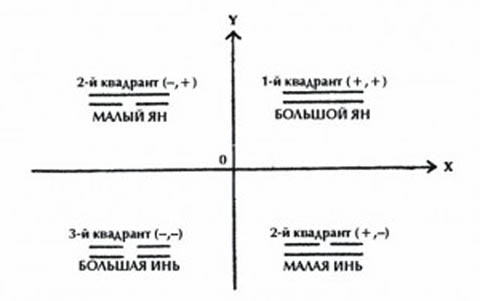
Рисунок 5
Если Ян – ноль, а Инь – единица, то свойства Четырех Символов, взятых по порядку, можно показать с точки зрения теории чисел (см. табл.1).
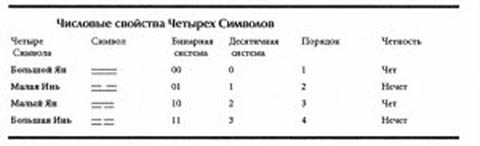
Таблица 1
Подобно тому как в аналитической геометрии для объяснения уравнений применяется графический способ, в системе Тайцзи различные категории представляются при помощи особых символов, состоящих из трех ярусов Инь- или Ян- черт. Эти символы известны как Восемь Триграмм (багуа).
С помощью Восьми Триграмм классифицируются все явления Вселенной, анализируются природные и социальные феномены. Это научный подход, ищущий взаимосвязи принципов, явлений и качеств. Форму Восьми Триграмм помогает запомнить древнее китайское мнемоническое стихотворение:
Цянь – Сшлошные
Кунь – Обломки
Чжэнь – Как чашка
Гэнь – Как шапка
Ли – Пустой центр
Кань – Центр полный
Дуй – Верх сломан
Сюнь – В дне дырка
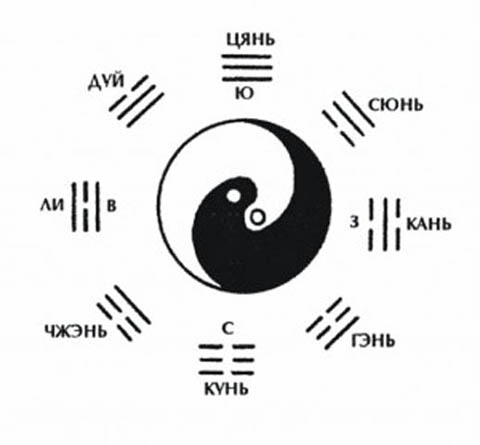
Рисунок 6
Восемь – максимальное число возможных комбинаций трех элементов, каждый из которых принадлежит к одному из двух типов.
Император Фу Си (2852 – 2738 гг. до н.э.) первым применил Восемь Триграмм к Диаграмме Тайцзи, чтобы показать взаимодействие Инь и Ян. Его вариант кругового расположения триграмм так и называется: Фу-Си, иначе Сяньтянь (что означает дословно “раннее небо” или “прежнее небо”, т.е. состояние, имевшее место до сотворения Вселенной).
Кроме описанных Восьми Триграмм Сяньтянь, существует и другой способ их расположения: Восемь Триграмм Хоутянь. Согласно легенде, их начертил Вэнь-ван, основатель династии Чжоу, примерно в 1143 г. до н.э. Он основывался на И-Цзине, где сказано:
“Правитель нисходит в Чжэнь, стобы начать свое творение. Он завершает все в Сюнь. Он проявляет вещи, чтобы они видели друг друга, в Ли, и побуждает их служить друг другу в Кунь. Он веселится в Дуй и сражается в Цянь. Он отдыхает и вкушает покой в Кань и завершает свои годичные труды в Гэнь”.
Итак, начиная с востока, Восемь Триграмм Хоутянь идут в следующем порядке по часовой стрелке: Чжэнь – Сюнь – Ли – Кунь – Дуй – Цянь – Кань – Гэнь. Эта последовательность объясняет принцип движения Вселенной и служит основой для китайского календаря:
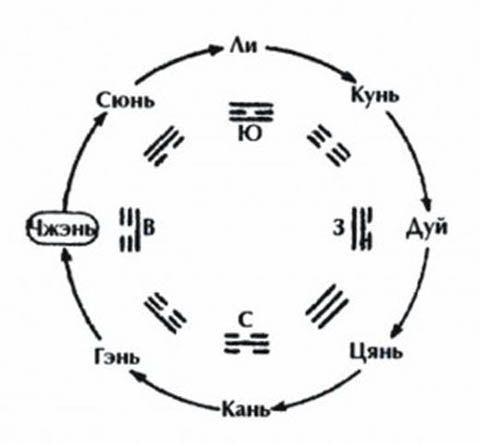
Рисунок 7
Можно при помощи наглядных схем показать, как Тайцзи образует Две Формы, Две Формы – Четыре Символа, а те – Восемь Триграмм. Здесь вы видите три такие схемы. Первая выполнена в виде таблицы (рис. 8), вторая – в форме древа (рис. 9), а третья – в форме круглой диаграммы (рис. 10).
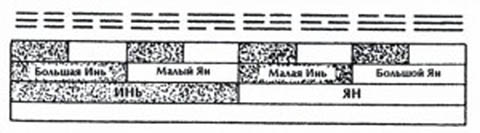
Рисунок 8
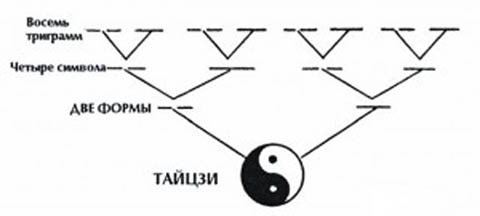
Рисунок 9
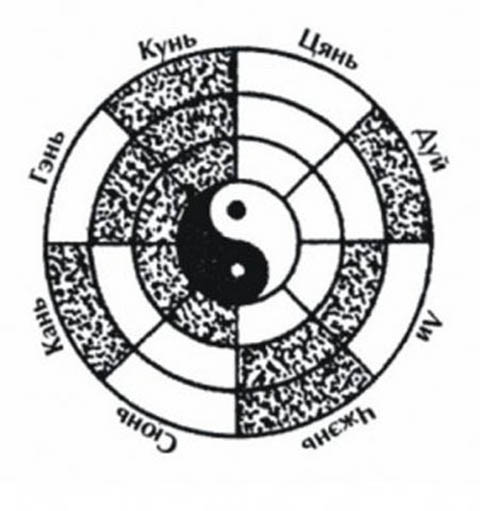
Рисунок 10
По принципам системы Тайцзи поддаются логическому описанию различные геометрические соотношения. Рис. 11 на примере трехосной системы пространственных координат показывает разницу между правосторонней и левосторонней системами:
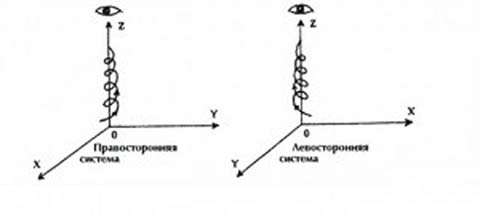
Рисунок 11
Как в право-, так и в левосторонней системе три координатные плоскости делят пространство на восемь октантов. Среди математиков нет еще единого мнения относительно нумерации октантов. Но если бы они приняли за Ян положительное направление каждой оси, а за Инь – отрицательное и воспользовались ВосЕмью Триграммами в порядке Сяньтянь или Хоутянь, то легко смогли бы установить порядок октантов (см. табл. 2).
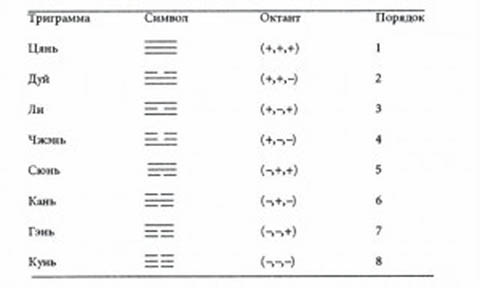
Таблица 2. Триграммы и октанты.
Как уже объяснялось при рассмотрении Четырех Символов, Ян = 0, Инь = 1. Триграмма читается снизу вверх. Прогрессия направлена так же, как в бинарной системе.
Например, Кань (Инь-Ян-Инь) соответствует 101 в бинарной системе или 5 в десятеричной. Если за основание берем n, то Кань представляет собой n^2 + 1. Таблица 3 показывает все эти соотношения.

Таблица 3. Числовые свойства Восьми Триграмм.
Бинарную, или двоичную систему счисления разработал в XIX веке немецкий математик Лейбниц. Но древние китайцы были знакомы с такой системой в виде Восьми триграмм) еще пять тысяч лет назад.
Каждая из триграмм не только является математическим символом, но и представляет различные объекты:

Таблица 4. Восемь Триграмм и их соответствия.























